正弦定理的四种证明方法(4)

∵BC CA=BA
∴n·（BC CA）=n·BA（两边同时与n作数量积）
∴n·BC n·CA=n·BA
∣n∣∣BC∣cos90° ∣n∣∣CA∣cos(90°-∠C)=∣n∣∣BA∣cos(90°-∠B)
b sin∠C=c sin∠B
∴b/sin∠B=c/sin∠C
同理可得a/sin∠A=b/sin∠B=c/sin∠C
（2）当△ABC为直角三角形时，不妨令∠B=90°

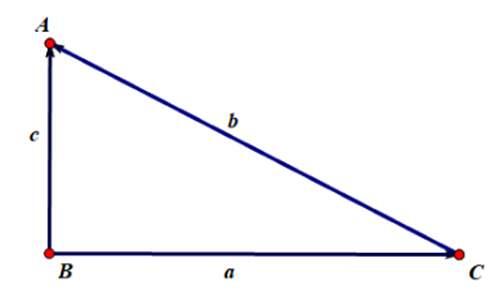
立即得a/sin∠A=b/sin∠B=c/sin∠C=b=2r=d(r为外接圆半径）
（3）当△ABC为钝角三角形时，不妨令∠B为钝角，作向量BC、BA、AC以及垂直于BC的向量n（以加粗表示向量），如下图