有趣的缺8数(3)
2023-03-16 来源:你乐谷
缺8数与乘数为3或9倍数(≥81)的部分乘积
首先,我们发现当缺8数乘以一个不是3或9倍数的数时,乘积的各位数字均不相同,但总是缺一个数字。而且缺的数字是呈现周期性的:8-7-5-4-2-1,就好像工厂轮休一样,比如我们继续往后写,缺8数乘以19,一定是缺8,乘以20,一定是缺7,乘以22一定是缺5,以此类推。
那么乘数之间有什么关系呢?对比上面两组式子,我们发现当缺少相同的数时,乘数之间相差为9的倍数。比如乘积缺少8的乘数可以为1,10,19,28……
10-1=9,
19-1=9×2
28-1=9×3
所以,发现了吗?下一个乘积缺少8的乘数一定是37。这样,我们就可以根据乘数判断乘积缺少什么数字了。我们举个例子:
12345679×68
我们可以先列一个式子:
68-a=9b
其中a为10以内不为3或9且不为0的正整数,b为9的正整数倍。那么,a的取值范围是0a10(a≠3,6,9,a∈N),0b10(b∈N )
那么,满足这个条件的解:b=7,a=5。
我们根据之前两组式子,可以断定这个式子的乘积所得数缺少数字4。
那么我们能不能直接计算出来结果呢?
也是可以的。我们观察
乘数相隔9,成绩得数顺序一样,位置不同
我们发现,当乘积所得数缺少的数字相同时,这个得数中总有一串数字的顺序是完全一样的,比如上面一组数中“1728395”、“06”这些数字的顺序是一样的,只是位置不一样。那么是什么影响了数字的位置呢?
就是乘积所得数的个位数,用一个式子来讲解下:
12345679×14
我们知道这个式子乘积的个位数一定是6。
首先我们先设定: (0)12345679× 5=(0)61728395为基础式,
在这个式子的乘积中找到6的位置,往后的下一位是1,所以乘积的第一个数就是1,后面直接抄——1728395,抄到最后数字没了,返回到基础式乘积的首位接着抄,就是172839506,也就是12345679×14这个式子的结果了,我们来看一下动图演示:
首先,我们发现当缺8数乘以一个不是3或9倍数的数时,乘积的各位数字均不相同,但总是缺一个数字。而且缺的数字是呈现周期性的:8-7-5-4-2-1,就好像工厂轮休一样,比如我们继续往后写,缺8数乘以19,一定是缺8,乘以20,一定是缺7,乘以22一定是缺5,以此类推。
那么乘数之间有什么关系呢?对比上面两组式子,我们发现当缺少相同的数时,乘数之间相差为9的倍数。比如乘积缺少8的乘数可以为1,10,19,28……
10-1=9,
19-1=9×2
28-1=9×3
所以,发现了吗?下一个乘积缺少8的乘数一定是37。这样,我们就可以根据乘数判断乘积缺少什么数字了。我们举个例子:
12345679×68
我们可以先列一个式子:
68-a=9b
其中a为10以内不为3或9且不为0的正整数,b为9的正整数倍。那么,a的取值范围是0a10(a≠3,6,9,a∈N),0b10(b∈N )
那么,满足这个条件的解:b=7,a=5。
我们根据之前两组式子,可以断定这个式子的乘积所得数缺少数字4。
那么我们能不能直接计算出来结果呢?
也是可以的。我们观察
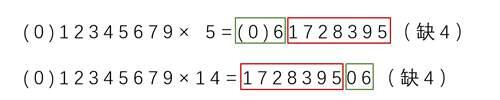
乘数相隔9,成绩得数顺序一样,位置不同
我们发现,当乘积所得数缺少的数字相同时,这个得数中总有一串数字的顺序是完全一样的,比如上面一组数中“1728395”、“06”这些数字的顺序是一样的,只是位置不一样。那么是什么影响了数字的位置呢?
就是乘积所得数的个位数,用一个式子来讲解下:
12345679×14
我们知道这个式子乘积的个位数一定是6。
首先我们先设定: (0)12345679× 5=(0)61728395为基础式,
在这个式子的乘积中找到6的位置,往后的下一位是1,所以乘积的第一个数就是1,后面直接抄——1728395,抄到最后数字没了,返回到基础式乘积的首位接着抄,就是172839506,也就是12345679×14这个式子的结果了,我们来看一下动图演示:

 女神级稀缺番号
女神级稀缺番号














