三角形基础知识 三角形的定义(3)
2023-03-16 来源:你乐谷
方案1:如图3所示,在BC上取D,E,F,使BD=DE=EF=FC,连接AD,AE,AF。
方案2:如图4所示,在BC边平均分成四份;D为一个等分点,连接AD。再将AD平均分成三份,等分点为E,F,连接CE,CF,即可分成面积相等的四个三角形。
方案3:如图5所示,取BC边D为两等分点,连接AD,再将BD,AD分别分成两等份,等分点为E,F,连接AE,CF,所得到的四个三角形面积相等。
【点评】利用“等底同高的三角形面积相等”的原理,三角形的中线可以将原三角形等分,在此基础上又可将分好的三角形再等分,以此类推,我们利用三角形的中线可达到将一个三角形若干等分或按比例分割的目的,且方法不唯一。
类型3 等腰三角形分割问题
例3 在等腰△ABC中,AB=AC,一边上的中线BD将这个三角形的周长分为15和12两个部分,则这个等腰三角形的底边长为
A.7 B.11 C.7或11 D.7或10
【分析】因为已知条件给出的15或12两个部分,哪一部分是腰长与腰长一半的和不明确,所以分两种情况讨论
【解答】不妨设等腰三角形腰长为x,底为y,已知条件并没有指明哪一部分是15,哪一部分是12,因此,可分两种情况,根据题意可列方程组
这个等腰三角形的底边长为7或11,线C
【点评】条件中没有明确给出哪一部分长,一定要想到两种情况,分类进行讨论,还应验证各自情况是否能构成三角形,这一点非常重要,也是解题的关键。
方案2:如图4所示,在BC边平均分成四份;D为一个等分点,连接AD。再将AD平均分成三份,等分点为E,F,连接CE,CF,即可分成面积相等的四个三角形。
方案3:如图5所示,取BC边D为两等分点,连接AD,再将BD,AD分别分成两等份,等分点为E,F,连接AE,CF,所得到的四个三角形面积相等。
【点评】利用“等底同高的三角形面积相等”的原理,三角形的中线可以将原三角形等分,在此基础上又可将分好的三角形再等分,以此类推,我们利用三角形的中线可达到将一个三角形若干等分或按比例分割的目的,且方法不唯一。
类型3 等腰三角形分割问题
例3 在等腰△ABC中,AB=AC,一边上的中线BD将这个三角形的周长分为15和12两个部分,则这个等腰三角形的底边长为
A.7 B.11 C.7或11 D.7或10
【分析】因为已知条件给出的15或12两个部分,哪一部分是腰长与腰长一半的和不明确,所以分两种情况讨论
【解答】不妨设等腰三角形腰长为x,底为y,已知条件并没有指明哪一部分是15,哪一部分是12,因此,可分两种情况,根据题意可列方程组
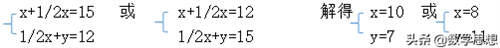
这个等腰三角形的底边长为7或11,线C
【点评】条件中没有明确给出哪一部分长,一定要想到两种情况,分类进行讨论,还应验证各自情况是否能构成三角形,这一点非常重要,也是解题的关键。
 cos av角色扮演合集
cos av角色扮演合集
