三角形基础知识 三角形的定义(2)

一．三角形的角平分线
在三角形中，一个内角的角平分线与它的对边相交，这个角的顶点与交点之间的线段，称为三角形的角平分线。
方法点拨
类型1 三角形高的分类讨论
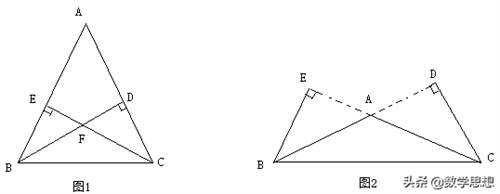
例1 若BD，CE是△ABC的高，BD，CE所在的直线相交所成的角中有一个角为55度，求∠BAC的度数
【分析】三角形的形状没有明确，故需分以下两种情况进行讨论，如图：

【解答】若△ABC是锐角三角形，如图1所示，因为BD，CE是△ABC的高，∠BAC=180- 180-55=55,所以∠BAC=55度
若△ABC是钝角三角形，如图2所示，因为BD，CE是△ABC的高，所以∠AEB=∠ADC=90度，
∴∠BAE=55度
∴∠BAC=125度
∴∠BAC为125度或55度
【点评】由于三角形高的分布与三角形形状有关，因而处理三角形的高有关问题时通常需要分类讨论。
类型2 面积的等分
例2 把任意三角形ABC平均分成面积相等的四个部分
【分析】三角形的中线可将三角形分成面积相等的两部分，其原理是等底同高，利用这个原理，我们可将三角形一边若干等分，进而达到将三角形的面积等分的目的。
【解答】本题答案不唯一，举例如下