paneldata数据分析 一(4)
2023-03-16 来源:你乐谷
混合回归模型方程式
这是最简单粗暴的处理方式,把所有的数据混合在一起,当做截面数据去对待,直接跑OLS.
尽管通常我们假设个体之间的扰动项相互独立,但是同一个体不同时间的扰动项存在自相关。这时候,对标准误的估计应该采用聚类稳健的标准误(cluster-robust standard error)。其中聚类(cluster)就是每个个体不同时期的所有观测值组成。同一聚类(个体)的观测值允许存在相关性,不同聚类个体的观测值则不相关。
因此,混合回归也被称为“总体平均估计量”(population-averaged estimator, PA),可以理解为化面板分析为截面分析。
混合回归的基本假设是不存在个体效应,也被认为是最严格的面板数据模型,在文献中不常见。(不常见的意思是不用学了,写paper也发不了)
这一假设的统计检验根据固定效应和随机效应进行检验。
2、个体固定效应模型(Inp>
我们假设给定个体i,个体之间有一些无法观测的异质性变量,用αi描述,比如说你想探索影响一个人升迁的因素,除了学历、专业等等可测变量,还有很多不可测的变量,如“guanxi”和情商等。
那么问题来了,个人的异质性因素αi是否会对回归元造成影响,也就是αi和x是否相关。如果相关,那就是固定效应模型,如果不相关,那就是随机效应模型。(这就是我们检验的依据)
2.1 固定效应模型(Fixed effects model (FE))
固定效应模型允许个体异质效应αi和回归元x相关
我们把αi归纳在截距中
每一个个体都有独自的截距项和相同的斜率
固定效应模型方程式
取估计去掉个体异质效果
这是最简单粗暴的处理方式,把所有的数据混合在一起,当做截面数据去对待,直接跑OLS.
尽管通常我们假设个体之间的扰动项相互独立,但是同一个体不同时间的扰动项存在自相关。这时候,对标准误的估计应该采用聚类稳健的标准误(cluster-robust standard error)。其中聚类(cluster)就是每个个体不同时期的所有观测值组成。同一聚类(个体)的观测值允许存在相关性,不同聚类个体的观测值则不相关。
因此,混合回归也被称为“总体平均估计量”(population-averaged estimator, PA),可以理解为化面板分析为截面分析。
混合回归的基本假设是不存在个体效应,也被认为是最严格的面板数据模型,在文献中不常见。(不常见的意思是不用学了,写paper也发不了)
这一假设的统计检验根据固定效应和随机效应进行检验。
2、个体固定效应模型(Inp>
我们假设给定个体i,个体之间有一些无法观测的异质性变量,用αi描述,比如说你想探索影响一个人升迁的因素,除了学历、专业等等可测变量,还有很多不可测的变量,如“guanxi”和情商等。
那么问题来了,个人的异质性因素αi是否会对回归元造成影响,也就是αi和x是否相关。如果相关,那就是固定效应模型,如果不相关,那就是随机效应模型。(这就是我们检验的依据)
2.1 固定效应模型(Fixed effects model (FE))
固定效应模型允许个体异质效应αi和回归元x相关
我们把αi归纳在截距中
每一个个体都有独自的截距项和相同的斜率
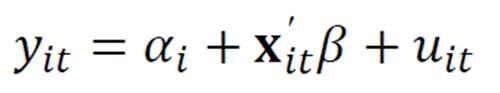
固定效应模型方程式
取估计去掉个体异质效果

 主题分类番号库
主题分类番号库










