欧拉恒等式的另一种解释(5)

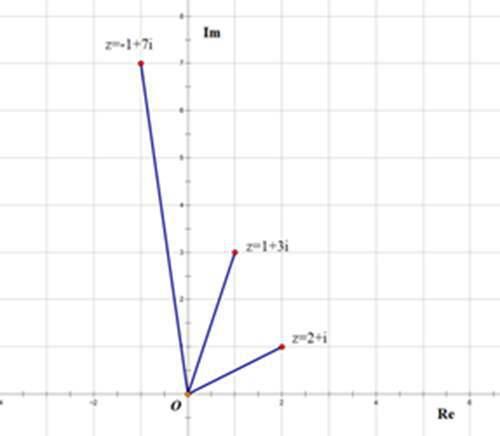
在复平面这三个复数显示如图

事实上，复数乘法有一个极好的几何意义，即复数z₁乘以z₂，在复平面上将z₁绕原点顺时针旋转θ角（其中θ为z₂的幅角），再将它的模长变为原来的|z₂|倍，就得到了结果复数所表示的点，例如上图，计算(1 i)(3 2i)，就是在复平面上将(1 i)绕原点顺时针旋转θ角（其中θ为(3 2i)的幅角），再将它的模长变为原来的|3 2i|=√ 13倍，就得到了结果复数所表示的点。
是不是觉得很神奇？那么现在换一种说法，有利于下面的继续说明。如图，计算(1 i)(3 2i)，就是在复平面上将(1 i)表示的点与1和0 表示的点所围成的三角形OIA绕原点顺时针旋转，使得OI与OB在同一条线上，得到三角形OI’A’，再将三角形OI’A’以原点为中心放大（或缩小），使得三角形OBA”，A”点表示的复数就是所得的结果。