切比雪夫多项式(7)
2023-03-16 来源:你乐谷
切比雪夫多项式是超球多项式或盖根堡多项式的特例,后者是雅可比多项式的特例。
切比雪夫多项式导数形式的递推关系可以由下面的关系式推出:
切比雪夫多项式在逼近理论中有重要的应用。这是因为第一类切比雪夫多项式的根(被称为切比雪夫节点)可以用于多项式插值。相应的插值多项式能最大限度地降低龙格现象,并且提供多项式在连续函数的最佳一致逼近。
切比雪夫多项式插值
切比雪夫多项式在逼近理论中有重要的应用。这是因为第一类切比雪夫多项式的根(被称为切比雪夫节点)可以用于多项式插值[1]。相应的插值多项式能最大限度地降低龙格现象,并且提供多项式在连续函数的最佳一致逼近。
幂级数项数的节约
设f(x)在(1,1)上的近似展开式为
切比雪夫多项式导数形式的递推关系可以由下面的关系式推出:
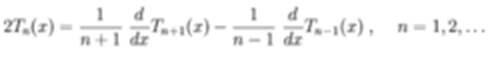
切比雪夫多项式在逼近理论中有重要的应用。这是因为第一类切比雪夫多项式的根(被称为切比雪夫节点)可以用于多项式插值。相应的插值多项式能最大限度地降低龙格现象,并且提供多项式在连续函数的最佳一致逼近。
切比雪夫多项式插值
切比雪夫多项式在逼近理论中有重要的应用。这是因为第一类切比雪夫多项式的根(被称为切比雪夫节点)可以用于多项式插值[1]。相应的插值多项式能最大限度地降低龙格现象,并且提供多项式在连续函数的最佳一致逼近。
幂级数项数的节约
设f(x)在(1,1)上的近似展开式为

 比较刺激的露出番号
比较刺激的露出番号







